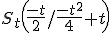| #k | kein Kreuz z. B. #kNormalparabel (Für Überschriften oder Beschriftungen) |
| #(TERM) | setze den aus TERM berechneten Wert ein. Der Term muss grundsätzlich in Klammern stehen. #(t+7) |
| #x bzw. #y | aktueller x bzw. y Wert (#x / #y) |
| #s | Strecke: Verbindet den Punkt mit dem vorhergehenden in der Liste |
| #v | verbinde Punktschar:kann nur verwendet werden, wenn der Punkt von einem Parameter abhängig ist. Glatteres Bild als #s, da Zwischenstellen berechnet werden. |
| #r=(TERM) | Zeichne Kreis um den Punkt mit Radius des berechneten Terms #r=(pi/4) oder #r=(t+1). Der Term muss in Klammern stehen |
| #r=(Termx; Termy) | Zeichne eine Ellipse um den Punkt. |
| #g=(ZAHL) | ZAHL ist Schriftgröße des Textes #g=(24) |
| ##f=(Arial) | Verwendung einer installierten Schriftart |
| #p | Polarkoordinaten: Die Koordinaten sind Winkel (phi) und Radius (r) |
| #zeiger(r;phi) | Zeiger mit der Länge R und der Phasenverschiebung phi. #zeiger(2;t*pi/4) |
| #qfehler | Die Summe der Quadrate der Abstände zwischen den Punkten und der aktuellen Funktion. Wichtiger Wert für die Güte einer Regression. Beachte: Dieser Punkt wird mitgezählt, sollte also einer der zu untersuchenden Punktmenge sein. |
Der Zeiger kann auch weitere Argumente haben, um die Interferenz in der Physik zu zeigen: Die Drehung des Zeigers hängt weiterhin von dem Abstand zu einem Punkt (x,y) und der Wellenlänge lambda ab.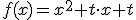 .
.